LAB

<latex>{\fontsize{16pt}\selectfont \textbf{Reachability Sets for Optimal Feedback Controllers}} </latex>

<latex>{\fontsize{12pt}\selectfont \textbf{Monitoring the Approach of a Region of Attraction}} </latex>
<latex>{\fontsize{10pt}\selectfont \textit{Master Project, RSC}} </latex>

---

<latex> {\fontsize{12pt}\selectfont \textbf{Abstract} </latex>

Sums-of-Squares optimization represents an important tool for the direct computation of a local Lyapunov function for a nonlinear dynamic system. Specifically, it can certify a sub-levelset of the cost-to-go from an optimal feedback controller like the Linear Quadratic Regulator (LQR), geometrically an ellipsoid in the state space, as Region of Attraction (ROA) of the closed-loop system.

More complex robotic tasks however require switching control to first take the system into the ROA before invoking the LQR stabilizer. We propose computationally efficient measures of the ROA distance based on quadratic and conic optimization to effectively supervise such a trajectory as it approaches the ROA. As a one-dimensional condensate of the multi-dimensional state trajectory, monitoring the ROA distance evolution allows us to early detect harmful deviations, e.g. due to input saturation or time delay, in order to quickly take corrective action such as replanning. Finally, we note that computing the ROA distance adds only a small overhead on top of the ROA calculation itself.

---

<latex> {\fontsize{12pt}\selectfont \textbf{Background} </latex>

A local Lyapunov function $V$ is a locally positive definite function (LPDF) on $B_r=\left\{x: \|x\| \le r\, \right\}$ such that $-\dot{V}$ is LPDF on $B_r$ and there is $\alpha>0$ such that $C=\left\{x|V(x)\leq \alpha\right\} \subset B_r$. A computationally feasible approach to establishing these properties relies on Sums-of-Squares (SOS) polynomials. Using $V(x) \; \textrm{SOS} \rightarrow V(x) \ge 0$ and $-\dot{V} \; \textrm{SOS} \rightarrow -\dot{V} \ge 0$, the SOS features provide sufficient conditions for the Lyapunov properties. For a closed-loop system, such results translate into stability guarantees of the controller. Moreover, SOS optimization can even compute a Region of Attraction (ROA), formally a sub-levelset $B(\rho) := \left\{x|0 \le V \le \rho\right\}$, in which the controller is guaranteed to stabilize the system.

^{1) 2)}

---

<latex> {\fontsize{12pt}\selectfont \textbf{ROA Distance} </latex>

For an LQR stabilizing controller, the sub-levelsets certified by SOS optimization as an ROA are ellipsoids in state space. This ellipsoidal shape can be used fruitfully for monitoring a trajectory as it approaches the ROA. For example, in the Euclidean distance metric, we find a convex quadratically constrained quadratic problem of the form $$ \min (x-p)^T (x-p), \;\;\; \textrm{subject~to} \;(x-x_0)^T A (x-x_0) \le 1\;\;\;\; \mathbf{(QCQP)}. $$ Primal-dual interior point methods such as SeDuMi or MOSEK can take full advantage not only of the problem's convexity but also the conic structure. The equivalent conic quadratic problem is $$ \min \mathbf{t},\;\;\; \textrm{subject~to} \;\left\{ \begin{array}{c}

(x-p)^T (x-p) \le \mathbf{t}\\
(x-x_0)^T A (x-x_0) \le 1

\end{array} \right.\;\;\;\; \mathbf{(CQP)}. $$ One can equally consider other distance metrics that lead to related optimization problems.

^{3) 4) 5)}

---

<latex> {\fontsize{12pt}\selectfont \textbf{A Sample Use Case} </latex>

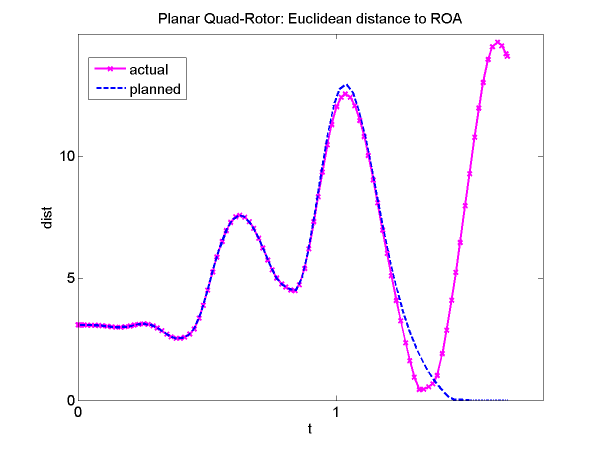
By comparing planned and actual ROA distance while a system follows a precomputed motion plan, we can detect when the system runs off-course and corrective action is required. As an illustrative example, consider the case of a previously undetected input saturation sabotaging the execution of the motion plan. As the system approaches the ROA, its ROA distance should follow the one derived from the motion plan and eventually converge to zero. However, as in the picture below, a significant excess of the planned distance signals the need for replanning.

The underactuated nonlinear system in the previous example has an eight-dimensional state space. The ROA distance thus condenses progress along the planned multi-dimensional state trajectory into a one-dimensional quantity that provides an informative measure and useful safeguard for detecting harmful deviations.

⁶⁾

---

<latex> {\fontsize{12pt}\selectfont \textbf{Software Implementation} </latex>

A significant challenge for a software implementation of ROA and ROA distance in a ROS environment is the efficient handling of SOS polynomial expressions. In particular, the number of contraints in the SOS program for the computation of the ROA itself grows at higher polynomial order with increasing state space dimension. On the other hand, the number of constraints in both QCQP and CQP formulations scales linearly with respect to the number of states. This appealing quality is the key reason for the efficiency of the ROA distance calculation as it adds little overhead on top of the ROA computation itself. An efficient conic solver such as MOSEK can even be used online.

^{7) 8) 9)}

---

<latex> {\fontsize{12pt}\selectfont \textbf{Summary} </latex>

At its core, this work contributes new ideas for supervising a dynamic motion plan for a nonlinear underactuated dynamical system. Our investigation considers complex tasks that require a switching controller providing initial dynamic motion followed by final stabilization of an equilibrium.

Sums-of-Squares optimization plays a key role for the direct computation of Lyapunov functions and the evaluation of stability regions in closed-loop dynamics. We observe that an optimal feedback controller like the Linear Quadratic Regulator gives rise to a Region of Attraction (ROA) of ellipsoidal shape in the state space. Exploiting this geometric constellation, we propose several measures of an ROA distance that can be cheaply computed using quadratic and conic optimization.

By experiments with common nonlinearities such as input saturation or time delay, we can demonstrate that tracking the ROA distance evolution permits us to early detect deviations that may otherwise harm robot hardware. In particular, computing the ROA distance adds only a small overhead on top of the ROA calculation itself.

We thus conclude that monitoring the ROA distance is a useful and affordable endeavor that allows us to rapidly resort to replanning when required by the situation at hand. Considering potential extensions and further applications, we envision our ideas to be applied to related more general settings such as LQR-Tree-based control as well as stabilization of limit cycles; this is future work.

¹⁰⁾